Yuan, Y., & Raubal, M. (2012). Extracting Dynamic Urban Mobility Patterns from Mobile Phone Data. In N. Xiao, M.-P. Kwan, M. F. Goodchild, & S. Shekhar (Eds.), Geographic Information Science (Vol. 7478, pp. 354–367). Springer Berlin Heidelberg.

1 Introduction

• urban structure has a strong impact on urban-scale mobility patterns, indicating that different areas inside a city are associated with different inhabitants’ motion patterns
• there has not been sufficient research on characterizing and classifying mobility patterns in different urban areas from a dynamic perspective
• We analyze the hourly patterns (time series) of mobility aggregation in different urban areas and demonstrate their differences

 

• reference area와 각 polygon의 temporal mobility를 비교

 

2 Related Work

2.1 Mobility Modeling and Mobile Phone Data

• Larsen identified five types of mobility
  • 1) Physical travel of people (e.g., work, leisure, family life) <- This research refers to "human mobility" as the first point.
  • 2) Physical travel of objects (e.g., products to customers)
  • 3) Imagination travel (e.g., memories, books, movies)
  • 4) Visual travel (e.g., internet surfing on Google Earth)
  • 5) Communication travel (e.g., person-to-person messages via telephones, letters, emails, etc.)
• individuals are atoms in an urban system, the spatiotemporal characteristics of an urban system could be viewed as a generalization of individual behavior
• Researchers have identified two major perspectives when exploring human mobility patterns from mobile phone data
  • Individual perspective: This category of research mainly focuses on identifying individual trajectory patterns
  • Urban perspective: Spatial division and morphology or Spatial clustering and spread
    
    • most previous research has concentrated on exploring aggregated patterns when analyzing urban mobility from mobile phone datasets
    • Here we focus on the temporal patterns of urban mobility

 

2.2 Dynamic Time Warping and Its Applications

• One important research question regarding time series data is finding whether two time series represent similar behavior
  • Euclidean distance: not suitable for measuring the distance between time series data
  • Discrete Fréchet Distance: very sensitive to outliers and displacements, therefore it is not very appropriate for time series data
  • Dynamic Time Warping (DTW): has been well developed to measure the similarity between time series
    • https://luckylucy.tistory.com/169

 

3 Research Design

3.1 Dataset

• a city in northeast China
• 9 days of data including one million mobile phone users
• time, duration, approximate location of mobile phone connections, age, and gender

 

3.2 Methodology

• DTW measures the similarity of hourly mobility patterns between different urban areas -> allowing us to group similar patterns together
• DTW shows a much better performance of distinguishing different time series than Euclidean or Fréchet

 

3.2.1 Summarize Dynamic Population from Cell Phone Records

• 1) divided the study area into Voronoi polygons based on the spatial distribution of cell phone towers
• 2) summarized the hourly phone call frequencies for each polygon
• 3) calculated relative mobility patterns for each polygon

 

3.2.2 Calculate DTW Distance Matrix

• 1) constructed the DTW distance matrix for the relative time series associated with each of the selected Voronoi polygons
• 2) used a global constraint “Sakoe-Chiba band”, which has a fixed window width in both horizontal and vertical directions
  • the window size is set to be 4, indicating that the maximum allowable absolute time deviation between two matched elements is 4 hours

 

3.2.3 Analyze Urban Mobility Patterns Based on DTW Distance Matrix

• conducted two example analyses for both circumstances based on the distance matrix
  • 1) mobility similarity to reference areas
  • 2) detecting outlier patterns

 

4 Data Analysis

4.1 Mapping the Similarity to Reference Areas

• Fig. 4 represents the similarity measure of mobility patterns between a reference polygon (marked red, where a major commercial street is located) and other urban areas
  • The dark brown color indicates a more similar mobility pattern (shorter DTW distance)
  • mobility patterns on weekdays are closer to the pattern in the reference area
  • we will need additional socioeconomic data to conduct additional correlation analyses

 

• Fig. 5 shows the distribution of DTW distances between the benchmark series [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1] and the study areas
  • polygons with a smaller DTW distance have more evenly distributed mobility patterns

 

• There are more polygons on weekends in the first group (DTW distance < 0.2) indicating that the mobility patterns on weekends are closer to an evenly distributed pattern

 

4.2 Outlier Detection

• Our objective is to identify cell polygons with abnormal mobility patterns
• Since hierarchical classification can operate directly on the distance matrix, we adopt this method to classify the mobility time series

 

• we detected 15 outliers for weekdays and 18 for weekends
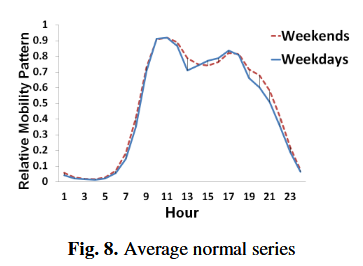
• Fig. 8 shows an average series for both weekdays and weekends after removing the outlier polygons
  • two mobility peaks each day

 

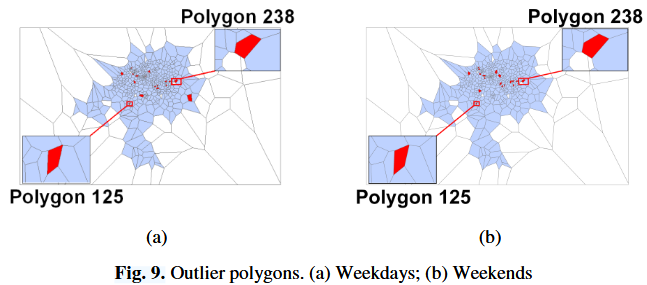
• Fig. 9 shows the results of the outlier detection
  • there are slight differences between weekdays and weekends

 

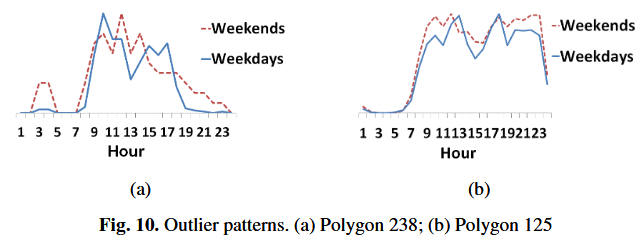
• Fig. 10 shows two examples of outlier time series
  • In polygon 238 there are many night clubs and other leisure facilities for night hours
  • In polygon 125 there are several community colleges and training schools