[기초통계] 통계적 추론–표본의 크기가 클 때–(모평균의 추정, 모평균에 대한 검정, 모비율에 대한 추론)

<통계학 : 파이썬을 이용한 분석> 책 내용 중 '10장. 통계적 추론' 부분을 요약하였고, 필요한 내용은 더 추가한 글임을 미리 밝힙니다.

 

 

7. 통계적 추론

 

10.1 서론

- 통계적 추론(statistical inference): 표본이 갖고 있는 정보를 분석하여 모수에 관한 결론을 유도하고, 모수에 대한 가설의 옳고 그름을 판단하는 것
    - 100% 확실하다고 할 수 없기 때문에, 그 결론의 부정확한 정도를 반드시 언급해야 함
- 통계적 추론은 관심에 따라 ‘모수의 추정’과 ‘모수에 대한 가설검정’으로 나뉨
    - e) 어떤 도시의 중학교 1학년 남학생 30명을 임의추출하여 키를 측정했을 때,
        - (1) $\mu$를 하나의 값으로 추정(점 추정)
        - (2) $\mu$를 포함할 만한 적당한 구간을 정함(구간추정)
        - (3) $\mu$ 값이 5년 전의 평균값인 155cm와 다른지 판단(가설검정)

 

---

10.2 모평균의 추정(표본의 크기가 클 때)

- 점추정(point estimation)
    - 추출된 표본으로부터 모수의 값에 가까우리라고 예상되는 하나의 값을 제시하는 것
    - 개념
        - 추정량(estimator): 모수를 추정하기 위해 만들어진 통계량
        - 추정치(estimate): 주어진 관측값으로부터 계산된 추정량의 값
            - e) 남학생 키 예시에서 표본평균의 값은 $\bar{X}=\frac{1}{n}(X_1+\cdots+X_n), \bar{x}=$160.20cm이므로 평균키 추정치는 160.20cm
        - 표준오차(standard error, S.E.): 추정량의 정확도를 측정하는 도구 중 하나이며, 값이 작을수록 바람직함
            - $S.E.(\bar{X})=\frac{\sigma}{\sqrt{n}}$, 추정된 표준오차: $\frac{s}{\sqrt{n}}$
- 구간추정(interval estimation)
    - 모수를 포함하리라고 예상되는 적절한 구간을 구하는 것
    - 개념
        - 신뢰구간(confidence interval): 추정량의 분포를 이용하여 표본으로부터 모수 값을 포함
        - 신뢰수준(level of confidence): 모수를 포함할 확률이며, 대개 90%, 95%, 99% 등을 사용
        - 오차범위(error margin)
    - 표본 크기가 크고 평균과 표준편차가 $\bar X$, $s$로 주어질 때 $\mu$에 대한 100(1-$\alpha$)% 신뢰구간은 다음과 같이 구함
        - $(\bar X-z_{a/2}\frac{s}{\sqrt n}, \bar X+z_{a/2}\frac{s}{\sqrt n})$ 혹은 $\bar X \pm z_{a/2}\frac{s}{\sqrt n}$다
        - 단, 모집단의 표준편차($\sigma$)가 알려져 있으면 $s$를 $\sigma$로 대체
    - 일반적으로 추정량의 기댓값이 추정하고자 하는 모수값을 갖고 그 분포가 정규분포일 때 100(1-$\alpha$)% 신뢰구간은 다음 형태를 따름
        - 추정량$\pm z_{a/2}\times$(표준오차)

 

---

10.3 모평균에 대한 검정(표본의 크기가 클 때)

- 가설검정(testing statistical hyphotheses): 추출한 표본으로 모수에 대한 가설이 적합한지 판단하고자 하는 것
- 개념
    - 가설(hypotheses)
        - 대립가설($H_1$): 입증하여 주장하고자 하는 가설
        - 귀무가설($H_0$): 대립가설의 반대 가설로, 대립가설을 입증할 수 없을 때 대립가설을 무효화시키면서 받아들이는 가설
- 오류의 종류
    - 제1종 오류(Type I error): 귀무가설이 맞을 때 귀무가설을 기각하는 오류
    - 제2종 오류(Type II error): 대립가설이 맞을 때 귀무가설을 기각하지 않는 오류
        - 일반적으로 우리가 무엇인가를 주장할 때 좀 더 확실한 근거를 바탕으로 주장을 하게 되며, 이는 1종 오류를 범하지 않으려고 하는 노력임
        - 검정에서도 대개의 경우 제1종 오류에 더 주의를 기울이게 됨

실제의 상태 \ 검정의 결론	$H_0$을 기각하지 않는다.	$H_0$을 기각한다.
$H_0$이 맞다 ($H_1$이 틀리다.)	옳은 결론	잘못된 결론(제1종 오류)
$H_0$이 틀리다 ($H_1$이 맞다.)	잘못된 결론(제2종 오류)	옳은 결론

(출처: <통계학: 파이썬을 이용한 분석)

- 검정통계량과 기각역의 결정
    - 검정통계량(test statistic): $H_{0}$을 기각하거나 기각하지 않을 때 이용하는 표본의 함수(통계량)
    - 기각역(critical region): 적당한 $c$에 대해서 $\bar X\leq c$일 때 $H_0$을 기각하게 되며, 기각하는 구간
        - 제1종 오류를 범하게 되는 확률: $\alpha$
        - 제2종 오류를 범하게 되는 확률: $\beta$
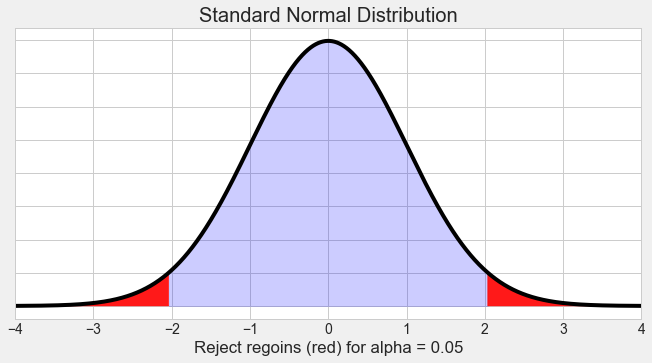
        - 이 두 확률을 최소화시키는 것이 가장 바람직한 기각역이며, 대개 1종 오류가 더 심각하기 때문에 $\alpha$값이 0.05, 0.1 또는 0.01 등 작은 값을 갖도록 상한선을 두고 $\beta$를 작게 해 주는 기각역을 선택함
    - 유의수준(significance level): 선택된 기각역의 $H_0$하에서의 확률($\alpha$)을 말함
    - Z-검정(Z-test)
        - 표본으로부터 직접 $Z$값을 구해서 $Z\leq-z_\alpha$가 성립하는가 여부를 가린 후, 검정 결론을 내리는 경우가 흔함
        - 검정통계량으로 $Z=\frac{\bar{X}-\mu_0}{s/\sqrt n}$ 사용, 기각역을 $R:Z\leq-z_\alpha$로 표현

(출처: https://ko.wikipedia.org/wiki/Z-테스트)

    

---

    10.4 모비율에 대한 추론(표본의 크기가 클 때)
    
    - 개념
        - 모수: 모집단에서 $A$라는 특성을 갖는 집단의 비율; 모비율 $p$
        - 자료: 크기가 $n$인 표본에서 $A$라는 특성을 갖는 개체의 수; $X$
        - 추정량: 표본비율; $\hat{p}=\frac{\bar X}{n}$
        - 표준오차: $S.E.(\hat p)=\sqrt{\frac{p(1-p)}{n}}$, 추정된 표준오차$\sqrt{\frac{\hat p(1- \hat p)}{n}}$
    - 모비율에 대한 신뢰구간
        - $(\hat{p}-z_{\alpha /2}\sqrt{\frac{p(1-p)}{n}}, \hat{p}+z_{\alpha /2}\sqrt{\frac{p(1-p)}{n}})$

 

 

통계학: 파이썬을 이용한 분석

오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파이썬은 빅데이터 처리에서 가장 많이 쓰이는 고급 프로그래밍 언어 중 하나로서 인터넷을 통해 무료로 또한, 지속적으로 새로운 함수 등이 업데이트되고 있어서 실제로 트렌디한 데이터 분석 및 여러 인공지능 관련 프로그래밍에서 필수적인 언어로 자리매김하는 중이다. 각 장 마지막 부분에는 파이썬을 이용한 예제를 제시하여 그 장에서 소개한 내용에 대한 예제를 따라하면서 언어와 분석 방법을 익힐 수 있도록 구성하였으며, 기본적인 파이썬에 대한 사용법은 부록에 수록하였다.

저자

인하대학교 통계학과

출판

자유아카데미

출판일

2022.06.25