[기초통계] 정규모집단에서의 추론(t 분포, 모평균에 대한 추론, 신뢰구간과 양측검정의 관계, 모표준편차에 대한 추론)

<통계학 : 파이썬을 이용한 분석> 책 내용 중 '11장. 정규모집단에서의 추론' 부분을 요약하였고, 필요한 내용은 더 추가한 글임을 미리 밝힙니다.

 

 

11. 정규모집단에서의 추론

 

11.2 $t$ 분포

- 정규모집단 $N(\mu, \sigma^2)$으로부터 임의추출된 표본을 $X_1, \cdots, X_n$이라고 할 때, 표본평균과 표본 분산을 $\bar X=\frac{\sum X_i}{n}$, $s=\frac{\sum(X_i-\bar X^2)^2}{n-1}$이라고 정의하면, 표준화된 확률변수 $t=\frac{\bar X-\mu}{s/\sqrt{n}}$는 자유도가 $(n-1)$인 $t$분포를 따르고, 이를 기호로써 $t(n-1)$로 표현함

 

---

11.3 모평균에 대한 추론

- 모집단이 정규분포를 따르고 모분산이 알려져 있지 않은 경우 t분포를 이용한 모평균에 대한 구간추정과 검정방법을 다룸
    - $\bar{X}±t_{\alpha/2}(n-1)\frac{s}{\sqrt n}$
    - $\sigma$가 알려져 있지 않은 경우, $s$로 추정함으로써 신뢰구간의 길이가 길어지는 경향이 있음
        - $z_{0.025}=1.96$, $t_{0.025}(4)=2.776$
        - 그러나 $n$이 커지며 $\sigma$도 $s$에 의해 더 정확하게 추정되고, $t_{\alpha /2}(n-1)$도 $z_{\alpha /2}$에 가까워져서 두 신뢰구간의 길이는 비슷해 짐
    - 표본의 크기가 작은 경우 모집단이 정규분포를 따른다고 가정하므로 정규분포가 맞는지 점검할 필요가 있음
    - 가설검정
        - 모분산이 알려지지 않은 경우, 검정통계량 $\frac{\bar X -\mu_0}{s/\sqrt n}$은 자유도가 $n-1$인 $t$분포를 따름
        - 표준정규분포표와 달리 $t$검정표는 몇 개의 $\alpha$값에 대해서만 상위 $\alpha$ 확률을 주는 값이 주어져 있기 때문에 정확한 $P-$값을 구하기 어려움

 

(출처: https://www.geeksforgeeks.org/students-t-distribution-in-statistics/)

 

---

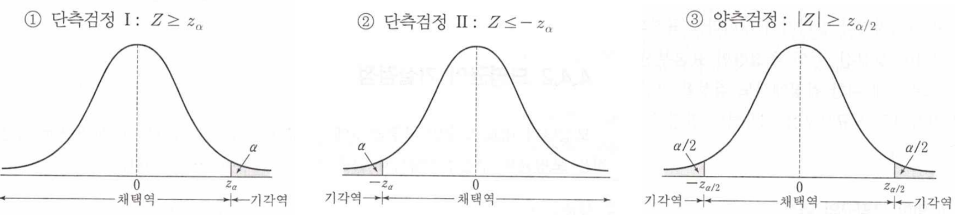
11.4 신뢰구간과 양측검정의 관계

- 모수 $\theta$에 대한 $100(1-\alpha)%$% 신뢰구간이 $(L, U)$로 구해졌을 때, 가설 $H_0: \theta=\theta_0$ 대 $H_1: \theta \neq \theta_0$에 대하여 유의수준 $\alpha$로 검정을 시행할 때 결론은 아래와 같음
    - $\theta \in (L, U)\Leftrightarrow H_0$를 기각할 수 없음
    - $\theta \notin (L, U)\Leftrightarrow H_0$를 기각함

 

(출처: http://kocw.xcache.kinxcdn.com/KOCW/document/2018/wonkwang/kimjunhui0410/13.pdf)

 

---

11.5 모표준편차에 대한 추론

- 모집단의 퍼져 있는 정도에 대해 추론하는 과정
    - e) 야구선수가 얼마나 안정적으로 자신의 타율을 유지하는지, 제품 생산에서 어느 정도 일정하게 제품의 무게나 크기를 유지하는지
    - 모표준편차 추론 전에, 모집단이 정규분포를 따르는지 먼저 확인해야 함
        - 모집단이 정규분포를 따르지 않는다면 t분포를 이용한 모평균 추론보다 심각한 오류를 범할 가능성이 더 높음
    - 모집단 표준편차($\sigma$)에 대한 추론은 모분산($\sigma^2$)에 대한 추론으로 시작함
        - $s^2=\frac{\sum{(X_i-\bar{X}})}{n-1}$ 활용
    - 점 추정의 경우, $\sigma^2$의 추정량으로 $s^2$ 사용
    - 구간 추정이나 검정의 경우, $s^2$의 분포가 필요 → ($\chi^2$ 분포와 연관 있음)
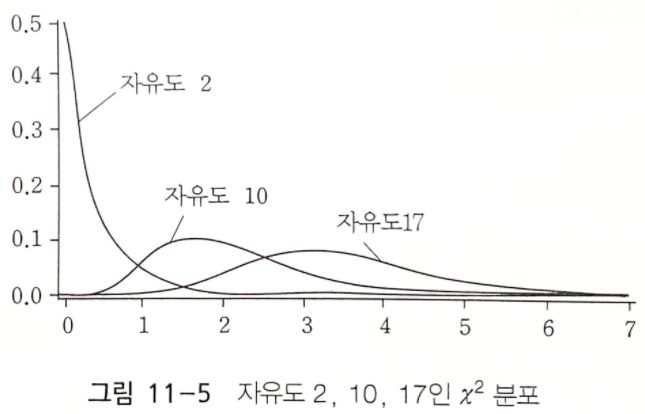
- $\chi^2$ 분포(chi-squared distribution)
    - 정규모집단 $N(\mu, \sigma^2)$으로부터 임의추출된 표본을 $X_1, \cdots, X_n$이라고 할 때, $\chi^2=\frac{\sum^{n}_{i=1}(X_i-\bar{X})^2}{\sigma^2}$은 자유도가 $(n-1)$인 $\chi^2$ 분포를 따르고, 이를 기호로써 $\chi^2(n-1)$로 표현
    - 확률밀도함수가 양수 쪽에만 퍼져 있고 오른쪽에 긴 꼬리를 갖는 비대칭형, 자유도가 클수록 0에서 멀리 떨어져서 넓게 분포

(출처: <통계학: 파이썬을 이용한 분석>)

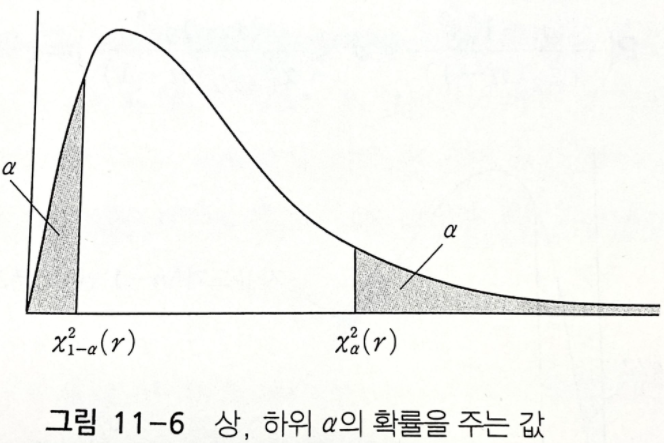
    - 자유도 $d.f.=r$에 대해 $\chi^2$분포의 상위 $\alpha$의 확률을 주는 값을 $\chi^{2}_{\alpha}(r)$로 표현하면, 자유도 $r$인 확률변수 $\chi^2$에 대하여 $P[\chi^2 \geq \chi^{2}_{\alpha}(r)]=\alpha$를 만족시킴

전형적인 $\chi^2$ 분포와 그에 대응되는 $\chi^{2}_{\alpha}(r)$ 와 $\chi^{2}_{1-\alpha}(r)$ (출처: <통계학: 파이썬을 이용한 분석>)

 

 

 

통계학: 파이썬을 이용한 분석

오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파이썬은 빅데이터 처리에서 가장 많이 쓰이는 고급 프로그래밍 언어 중 하나로서 인터넷을 통해 무료로 또한, 지속적으로 새로운 함수 등이 업데이트되고 있어서 실제로 트렌디한 데이터 분석 및 여러 인공지능 관련 프로그래밍에서 필수적인 언어로 자리매김하는 중이다. 각 장 마지막 부분에는 파이썬을 이용한 예제를 제시하여 그 장에서 소개한 내용에 대한 예제를 따라하면서 언어와 분석 방법을 익힐 수 있도록 구성하였으며, 기본적인 파이썬에 대한 사용법은 부록에 수록하였다.

저자

인하대학교 통계학과

출판

자유아카데미

출판일

2022.06.25