[기초통계] 이항분포와 그에 관련된 분포들(베르누이 시행, 이항분포, 초기하분포, 포아송분포)

<통계학 : 파이썬을 이용한 분석> 책 내용 중 '7장. 이항분포와 그에 관련된 분포들' 부분을 요약하였고, 필요한 내용은 더 추가한 글임을 미리 밝힙니다.

 

 

7. 이항분포와 그에 관련된 분포들

 

7.2. 베르누이 시행(bernoulli trial)

- 매번 반복되는 추출(실험)을 시행(trial)이라고 하고, 두 개의 가능한 결과 중 하나는 성공(success, $S$), 다른 하나는 실패(failure, $F$)라고 부름
    - 이는 시행의 결과가 두 개 뿐임을 강조하는 의미이며 보통의 성공과 실패의 의미와는 무관
- 이러한 시행이 반복되며 아래 조건을 만족시키는 경우, 이를 베르누이 시행이라 부름
    - (1) 각 시행은 성공($S$), 실패($F$)의 두 결과만을 가짐
    - (2) 각 시행에서 성공한 확률은 $P(S)=p$, 실패한 확률은 $P(F)=q(=1-p)$로 값이 일정함
    - (3) 각 시행은 서로 독립으로 각 시행의 결과가 다른 시행의 결과에 영향을 미치지 않음
- e) 동전던지기 시행
    - 완전한 대칭의 동전을 던질 경우 $p=q=1/2$이며 각 시행은 독립임
- 복원추출과 비복원추출
    - 복원추출: 각 추출의 결과는 두 가지 뿐이며, 성공할 확률이 일정하며, 매 추출의 결과가 독립인 경우 베르누이 시행을 따른다고 할 수 있음
    - 비복원추출: 두 번째 추출의 결과가 첫 번째 추출의 결과에 영향을 받으므로 (3)번 조건을 만족시키지 못하지만, 모집단의 크기가 표본의 크기에 비해 상당히 크면(약 20배) 독립성의 위반은 아주 미약해져서 베르누이 시행 모형을 적용할 수 있음

 

---

7.3 이항분포(binomial distribution)

- 성공 확률이 $P$인 베르누이 시행을 $n$번 반복할 때 일어나는 성공의 횟수를 $X$라고 하면, 이 확률변수 $X$의 확률분포를 모수가 $(n, p)$인 이항분포라고 함
    - $X$~$Bin(n, p)$로 표현
    - $n$: 베르누이 시행의 반복 횟수
    - $p$: 각 시행에서 성공할 확률, $P(S)$
    - $X$: $n$번 시행 중 성공의 횟수
- 확률변수 $X$의 분포가 $X$~$Bin(n, p)$일 때, $x=0, 1, \cdots, n$에 대하여 확률질량함수는 $P(X=x)={n \choose x}p^xq^{n-x}$
    - $X$가 취하는 값의 범위는 $0, 1, \cdots, n$
    - $X$가 0일 확률은 $n$번의 독립 시행이 모두 실패할 확률이므로 $P(X=0)=q \times \cdots \times q=q^n$
    - $X$가 1일 확률은 ${n \choose 1}=n$에 각 확률 $pq^{n-1}$을 곱한 것으로 $P(X=1)=npq^{n-1}$
        - 단, ${n \choose k}={_nC_k}$

- 이항분포표에는 각 $n(=1,\cdots, 25)$과 $p(=0.1, \cdots, 0.9)$의 경우, 임의의 $c=0, 1,\cdots, n$에 대하여 $P(X\leq c)$가 주어져 있음

이항분포표 예시(출처: https://www.oreilly.com/library/view/understanding-business-statistics/9781118145258/26_app-A.html)

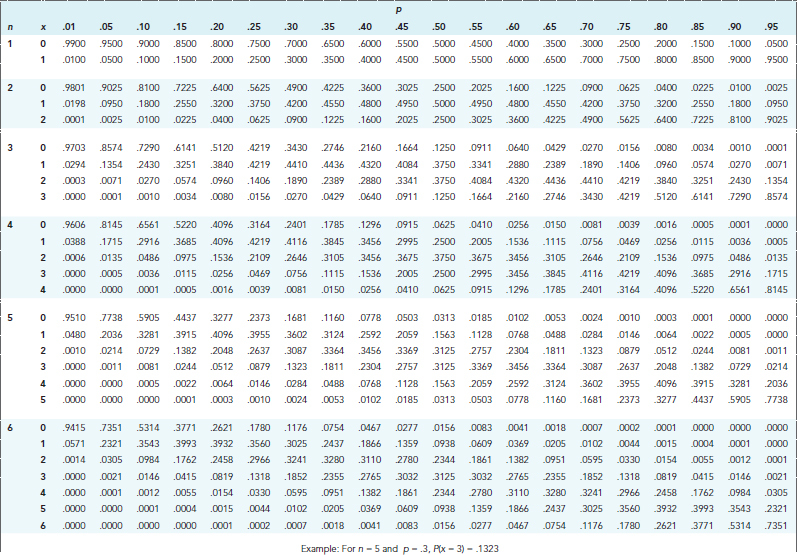
- 임의의 정수 $a, b$에 대하여 다음을 만족함
    - $P(X=a)=P(x\leq a)-P(X\leq a-1)$
    - $P(X\geq a)=1-P(X\leq a-1)$
    - $P(a\leq X \leq b)=P(X\leq b)-P(X\leq a-1)$
    - $P(a<X<b)=P(X\leq b-1)-P(X\leq a)$
- 이항분포의 기댓값, 분산, 표준편차
    - 기댓값: $E(X)=np$
    - 분산: $Var(X)=npq$
    - 표준편차: $sd(X)=\sqrt{npq}$

 

---

7.4 초기하분포(hypergeometric distribution)

- 유한한 모집단에서 비복원추출하는 경우, 성공의 횟수를 $X$라고 할 때 확률변수 $X$의 분포
    - $N$: 모집단의 크기
    - $n$: 표본의 크기
    - $D$: 모집단 내에서 범주 A에 속하는 구성원소의 수
    - $X$: 표본 내에서 범주 A에 속하는 구성원소의 수
- 초기하분포의 확률질량함수는 $P(X=x)={D \choose x}\times{N-D \choose n-x}/{N \choose n}, x=0, 1, \cdots, n$
    - 이때 $n$은 $D$나 $(N-D)$보다 작거나 같은 수라고 가정

 

---

7.5 포아송분포(poisson distribution)

- 매 순간 사건 발생이 가능하지만, 매 순간의 사건 발생 확률이 아주 작을 때 사용
    - e) 119 구조대에 시간당 걸려오는 전화횟수, 국내에서 발생하는 진도 4 이상 지진 횟수, 프러시아 기병 중 매년 말에 머리를 차여 사망하는 병사의 수
- 포아송분포를 적용하기 위해서 다음 가정을 만족해야 함
    - (1) 주어진 구간에서 사건의 평균 발생횟수의 확률분포는 구간의 시작점에는 관계가 없고 구간의 길이에만 영향을 받음
    - (2) 한 순간에 2회 이상의 사건이 발생할 확률은 거의 0에 가까움
    - (3) 한 구간에서 발생한 사건의 횟수는 겹치지 않는 다른 구간에서 발생하는 사건의 수에 영향을 받지 않음
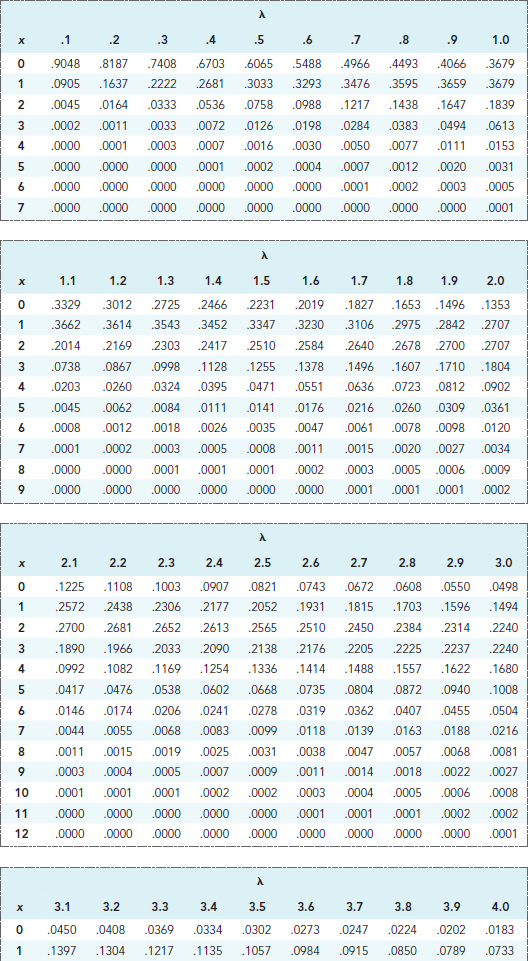
- 확률변수 $X$가 평균이 $m$인 포아송분포를 따른다고 하면 확률질량함수는 $P(X=x)=\frac{3^{-m}m^x}{x!}, x=0,1,\cdots$
- 포아송분포표에는 $m$의 값에 따라 음이 아닌 정수 $c$에 대하여 $P(X\leq c)$의 값이 주어져있음

포아송 분포표 예시(출처: https://www.oreilly.com/library/view/understanding-business-statistics/9781118145258/26_app-A.html)

 

 

통계학: 파이썬을 이용한 분석

오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파이썬은 빅데이터 처리에서 가장 많이 쓰이는 고급 프로그래밍 언어 중 하나로서 인터넷을 통해 무료로 또한, 지속적으로 새로운 함수 등이 업데이트되고 있어서 실제로 트렌디한 데이터 분석 및 여러 인공지능 관련 프로그래밍에서 필수적인 언어로 자리매김하는 중이다. 각 장 마지막 부분에는 파이썬을 이용한 예제를 제시하여 그 장에서 소개한 내용에 대한 예제를 따라하면서 언어와 분석 방법을 익힐 수 있도록 구성하였으며, 기본적인 파이썬에 대한 사용법은 부록에 수록하였다.

저자

인하대학교 통계학과

출판

자유아카데미

출판일

2022.06.25