1. 공간적 자기 상관성
공간적 자기 상관성은 지리적 인접성(geographical proximity)을 전제로, 하나가 변하면 다른 하나도 변하는 관계의 정도를 의미한다. 이 변화는 같은 방향(양의 자기 상관) 또는 반대 방향(음의 자기 상관)일 수 있다. 공간적 자기 상관성은 인과관계를 암시하지만 확립하지는 않는다.
공간적 자기 상관성을 정량적으로 측정하기 위하여 다양한 지수들이 제안되었으나, 가장 보편적으로 활용되는 통계지수 중 하나는 Moran’s $I$ 통계량(이후 $I$ 통계량)이다.
2. Moran's $I$
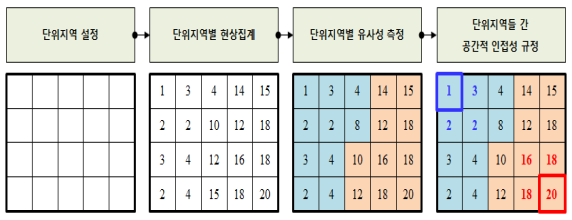
$I$ 통계량을 계산하기 위해서는 네 단계의 절차가 필요하다.
첫째, 분석대상지를 일정한 형태 및 크기의 공간분석단위(spatial analysis unit)로 분할한다.
둘째, 지리적 공간상에서 발생하는 현상을 단위지역별로 집계한다.
셋째, 단위지역별로 집계한 결과들 간 유사성을 측정한다.
넷째, 단위지역들 간 지리적 공간상에서의 인접성(spatial adjacency)을 규정한다.
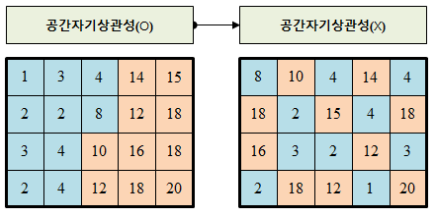
왼쪽 그림은 비슷한 값을 가지는 단위지역끼리 인접하려는 경향, 즉 공간적 자기 상관성이 있음을 보여준다. 반면, 오른쪽 그림은 공간적 자기 상관성이 없고 랜덤하게 분포하고 있음을 보여준다.

그림에서 (가)는 큰 값과 작은 값들이 규칙적으로 분포하는 패턴을 나타내며, 음의 공간적 자기 상관성을 보이는 것으로 해석한다. (나)는 패턴이 보이지 않는 랜덤 패턴을 나타낸다. (다)는 유사한 값들이 연속적으로 배열된 클러스터로, 양의 공간적 자기 상관성을 가지는 것으로 해석한다.
$I$ 통계량은 전역적 $I$ 통계량(global $I$ statistic)과 이를 구성하는 국지적 $I$ 통계량(local $I$ statistic)으로 구분된다. 전역적 $I$ 통계량은 전체 단위지역에서 나타나는 전반적인 경향을 나타내는 반면, 국지적 $I$ 통계량은 특정 단위지역을 중심으로 주변 단위지역들이 얼마나 비슷한 값을 가지는지 분석한다.
3. 전역적 $I$ 통계량
(1) 수식
$I=\frac{n\sum^{n}_{i=1}\sum^{n}_{j=1}w_{ij}(x_i-\bar x)(x_j-\bar x)}{(\sum^{n}_{i=1}\sum^{n}_{j=1}w_{ij})\sum^{n}_{i=1}(x_i-\bar x)^2}$
$n$: 단위지역의 개수
$x_i$: 단위지역 $i$에서 관찰 값
$\bar x$: 모든 단위지역이 갖는 값의 평균
$w_{ij}$: 단위지역 $i$와 $j$의 공간가중치 값(예로, 인접하면 1, 그렇지 않으면 0으로 정의한다)
$I$ 통계량의 실질적인 핵심 요소는 분자를 구성하는 요소인 $w_{ij}(x_i-\bar x)(x_j-\bar x)$이다. 두 단위지역 $i$와 $j$가 인접한 경우 즉, $w_{ij}=1$인 경우 두 단위지역 값들이 평균으로부터 멀어지려는 성향이 어느 정도 비슷한지를 나타내기 위한 일종의 공분산(covariance)에 해당한다. 즉, 단위지역 $i$의 값이 평균보다 큰 값을 가지는데 $i$와 인접한 $j$에서도 평균보다 큰 값을 가진다면 $w_{ij}(x_i-\bar x)(x_j-\bar x)$의 값은 커질 것인데, 만일 이러한 공분산 경향이 대상지 내 서로 인접한 단위지역 쌍들에서 많이 나타난다면 위 식의 값 역시 증가할 것이다. 이는 인접한 단위지역들 간 비슷한 값을 가지려는 경향이 우세함 즉, 공간적 자기 상관성이 강하게 나타남을 의미한다.
반대로, 단위지역의 값이 평균보다 작더라도 인접한 지역에서 평균보다 작은 값을 가지면 위 식의 값이 커지며, 이 또한 공간적 자기 상관성이 우세하다고 볼 수 있다. 두 단위지역이 인접하지 않은 경우에는 $w_{ij}=0$이 되므로 위 식의 공분산 요소에 아무 영향을 미치지 않는다.
$I$ 통계량은 -1과 +1 사이의 값을 가지며, +1에 가까울수록 양의(positive) 공간적 자기 상관성이 강하게 나타남을 의미하고, -1에 가까울수록 음의(negative) 공간적 자기 상관성이 크게 나타나는 것으로 해석할 수 있다. 이론적으로는 +1는 완벽한 양의 공간적 자기 상관패턴, -1은 완벽한 바둑판 패턴을 의미한다.
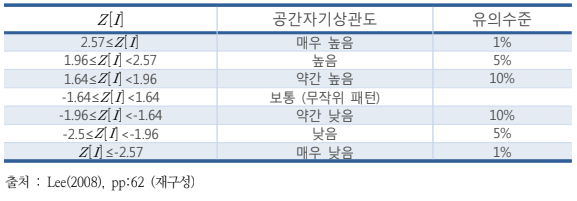
그러나 -1~+1 사이의 값만으로 판단하기 어려운 경우가 많은데, $I$를 표준화하여 $Z[I]$ 값을 통해 통계적 유의성과 관련된 보편적 명확한 해석기준을 적용할 수 있다.
$I$의 평균, 분산은 아래와 같고,
$E[I]=-\frac{1}{n-1}$
$V[I]=\frac{n^2(n-1)S_1-n(n-1)S_2+2(n-2)S^2_0}{(n+1)(n-1)^2S^2_0}$
단, $S_0=\sum^n_i\sum^n_{j\neq1}w_{ij},\space S_1=\frac{1}{2}\sum^n_i\sum^n_{j\neq1}(w_{ij}+w_{ji})^2, \space S_2=\sum^n_k(\sum^n_jw_{kj}+\sum^n_iw_{ij})^2$
$z-$ 값은 $Z[I]=\frac{I-E[I]}{\sqrt {V[I]}}$로 구할 수 있다.
(2) 예시
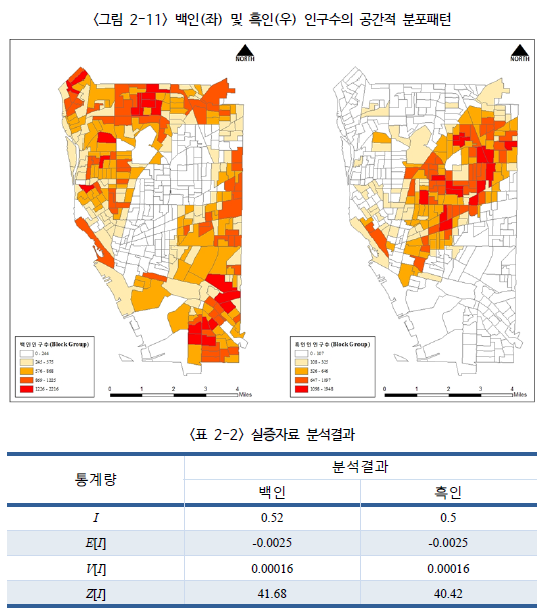
백인과 흑인 인구의 배타적 공간 분포 패턴을 예시로 살펴볼 수 있다.
$I$ 통계량이 각각 0.52, 0.5이므로 백인은 백인끼리, 흑인은 흑인끼리 거주하는 큰 공간적 자기 상관성이 있음을 추측할 수 있다.
$z-$값은 각각 41.68, 40.41인데, 이는 두 $I$ 값들이 우연에 의한 결과가 아님을 증명한다. 유의 수준 1% 조건 하에서 $z-$값이 2.57이므로, 통계적으로 매우 유의하다고 볼 수 있다.
Moran's I 결과는 지도로 표현되지 않고 통계값으로만 확인할 수 있다.
3. 국지적 $I$ 통계량(LISA, Local Indicators of Spatial Association)
(1) 수식
$I_i=\frac{(x_i-\bar x)}{S_x}\sum^{n}_{j\neq i}w_{ij}\frac{(x_j-\bar x)}{S_x}, \space S_x=\sqrt{\frac{\sum^{n}_{i=1}(x_i-\bar x)^2}{n-1}}$
공간단위별 변량을 $z-$값(표준정규분포 확률변수)으로 변환한 뒤 공간단위에 $i$에서의 $z-$값에다 $i$와 인접한 모든 공간단위 $j$에서의 $z-$값을 곱한 뒤 이들을 합산한 값이다.
$I_i$의 평균, 분산은 아래와 같고,
$E[I_i]=-\frac{\sum^n_{j=1}w_{ij}}{n-1}$
$V[I_i]=\frac{w_{i(2)}(n-b_2)}{n-1}+\frac{2w_{i(kh)}(2b_2-n)}{(n-1)(n-2)}-\frac{w^2_i}{n-1}$
단, $b_2=\frac{m_4}{m^2_2},\space m_r=\frac{\sum^n_{i=1}z^r_i}{n}, \space w_{i(2)}=\sum^n_{j=1}w^2_{ij},\space 2w_{i(kh)}=\sum^n_{k=1}\sum^n_{h=1}w_{ik}w_{ih}, \space j,k,h \neq i$
$z-$ 값은 $Z[I_i]=\frac{I_i-E[I_i]}{\sqrt {V[I_i]}}$로 구할 수 있다.
단위지역 주변에 유사한 값들이 군집해 있으면 $I_i$는 큰 값을 가지고, 반대의 경우 작은 값을 가지게 된다. 모든 단위지역을 대상을 $I_i$를 계산하고 $Z[I_i]$로 표준화 한 뒤 단계구분도로 시각화할 수 있다.
(2) 예시
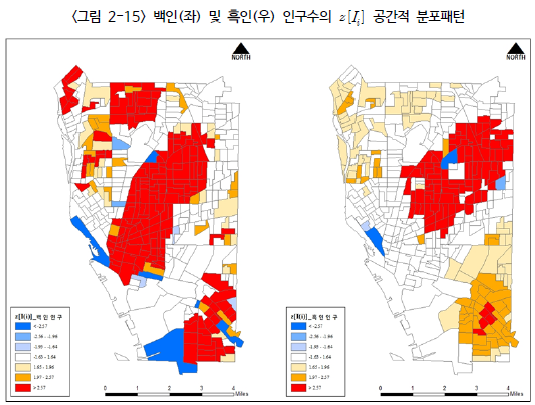
위 그림은 국지적 공간 자기 상관성을 $z-$값으로 추정하고 시각화한 결과이다. 유사한 값이 공간적으로 군집하려는 경향이 강할수록 빨간색, 다른 값들이 분포하는 지역일수록 파란색으로 표현되었다.
지도 왼쪽(백인)의 경우, 북동쪽에서 남서쪽을 가로지르며 가운데 지역을 중심으로 강한 공간적 자기 상관성이 나타나고 있다. 그림 2-11를 보면 이 지역은 백인들이 많이 거주하지 않는 지역이기 때문에, 작은 값들이 모여 있어서 강한 공간적 자기 상관성이 나타난 것이다. 또한, 북서쪽과 남동쪽에는 백인들이 많이 거주하기 때문에 높은 값들이 모여 있어서 강한 공간적 자기 상관이 나타났다. (즉, '높은 값'들의 모임은 우리가 아는 '핫스팟(높은 값들의 모임)'의 개념과는 다르다. 주변과 비슷한 값을 가져서 높은 $z$값을 가진 것이다.)
지도 오른쪽(흑인)의 경우, 중간 지역에 많이 거주하여 높은 공간적 자기 상관성이 나타났고, 북서쪽과 남동쪽에는 거의 거주하지 않기 때문에 낮은 값들의 공간적 자기 상관성이 나타났다.
정리하자면, local Moran's I 또는 LISA는 해당 공간단위와 주변에서 비슷한 값이 나타나기만 하면 높은 값으로 측정된다. 따라서, 실제 데이터 값은 알 수 없고 해당 공간단위와 주변의 값이 '유사한지'만 알아낼 수 있다.
Moran's I, local Moran's I로 공간적 자기 상관성을 확인했다면, 공간적 자기 상관이 높게 나타난 지역이 높은 값들의 모임인지, 낮은 값들의 모임인지는 Getis-Ord's $G$ , $G_i$ 등의 분석으로 확인할 수 있다.
[참고 자료]
이경주, 황명화, 한선희, & 양은정. (2015). 공간통계 분석의 이해와 활용을 위한 첫걸음.
Anselin, L. (1995). Local indicators of spatial association—LISA. Geographical analysis, 27(2), 93-115. link
De Smith, M. J., Goodchild, M. F., & Longley, P. (2021). Geospatial analysis: a comprehensive guide to principles, techniques and software tools. Troubador publishing ltd. link
'GIS > Spatial Analysis' 카테고리의 다른 글
| Gravity model for spatial decay effect (0) | 2024.11.04 |
|---|---|
| Density-Based Spatial Clustering of Applications with Noise (DBSCAN) 밀도 기반 클러스터링 (0) | 2024.10.24 |
| Dynamic Time Warping (DTW) with trajectory data 시계열 분석 (0) | 2024.09.28 |
| Moran's I와 Getis-Ord Gi*의 차이점 (0) | 2023.07.12 |
| Two-Step Floating Catchment Area, 2SFCA 접근성 분석 (0) | 2023.03.27 |



