[기초통계] 확률(사건의 확률, 확률의 계산, 확률법칙, 조건부확률과 독립성)

<통계학 : 파이썬을 이용한 분석> 책 내용 중 '5장. 확률' 부분을 요약하였고, 필요한 내용은 더 추가한 글임을 미리 밝힙니다.

 

5. 확률

5-2. 사건의 확률

- 사건의 확률

    - 그 사건이 일어날 가능성의 정도를 나타내 주는 수치

    - 동일한 조건에서 실험을 반복할 때 전체 실험 횟수에서 그 사건이 일어날 것이라 예상되는 횟수의 비율

    - 사건 $A$의 확률은 $P(A)$로 표현

 

- 개념

    - 표본공간(sample space: $Ω$): 한 실험에서 나올 수 있는 모든 결과들의 모임
    - 근원사건(elementary outcomes: $w_1, w_2, \cdots$) 표본공간을 구성하는 개개의 결과
    - 사건(event: $A, B, \cdots$): 표본공간의 부분집합으로 어떤 특성을 갖는 결과들의 모임(즉, 근원사건들의 집합)

표본공간, 근원사건, 사건 모식도, 직접 작성

 

- 표본 공간은 유한할 수도, 무한할 수도 있음. 표본공간의 원소가 연속체(continuum)로 주어져 나열할 수 없는 경우를 연속표본공간(continuous sample space)이라고 함.

 

- 확률의 법칙
    - (1) 모든 사건 $A$에 대하여 $0≤P(A)≤1$
    - (2) $P(A)=\sum_{w_1\in A}P(w_i)$
    - (3) $P(Ω)=\sum_{w_1\in Ω}P(w_i)$

 

---

 

5.3 확률의 계산

- 규칙 1(균일 확률)

    - 표본공간 $Ω$가 $k$개의 원소로 이루어져 있고 각 근원사건이 일어날 가능성이 동일(equally likely)할 때, 근원사건 하나가 일어날 확률은 $1/k$

    - 사건 A가 m개의 근원사건으로 이루어져 있다면 $P(A) = \frac{m}{k}=\frac{A에 속하는 근원사건의 개수}{Ω에 속하는 근원사건의 개수}$

 

- 규칙 2(상대도수 수렴치로서의 확률)

    - 동일한 실험을 $N$회 반복할 때 사건 $A$의 상대도수

    - $r_N(A)=\frac{N번의 시행 중 A가 일어난 횟수}{N}$

    - 여기에서 $N$이 증가함에 따라 상대도수가 일정한 값으로 수렴하면 그 값으로 $P(A)$를 추정

 

---

 

5.4 확률법칙

- 개념
    - 여사건: $A$에 포함되지 않은 근원사건들의 모임. $A^C$
    - 합사건: $A$ 또는 $B$에 포함되는 근원사건들의 모임. $A\cup B$
    - 곱사건: $A$와 $B$에 동시에 포함되는 근원사건들의 모임. $A \cap B$
    - 배반사건(disjoint event): 동시에 일어날 수 없는 사건

(출처: https://www.class.orbi.kr/00031464275)

 

- 여사건의 확률법칙: $P(A^C)=1-P(A)$

 

- 드모르간의 법칙
    - $(A\cap B)^C=A^C\cup B^C$
    - $(A\cup B)^C=A^C\cap B^C$

 

- 차집합의 성질: $A-B=A\cap B^C$

 

- 합사건의 확률법칙
    - 사건 $A$와 $B$가 배반사건이라면 $P(A \cap B)=P(∅)=0$
    - $P(A\cup B)=P(A)+P(B)$가 됨

 

---

 

5.5 조건부확률과 독립성

- 조건부확률

    - 사건 B에 관한 정보(사전정보: prior information)가 주어졌을 때 사건 A의 교정된 확률

    - $P(A|B)=\frac{P(A\cap B)}{P(B)}(단, P(B)>0)$

 

- 곱사건의 확률법칙: $P(A\cap B)=P(A|B)\times P(B)$

 

- 독립

    - 두 사건의 발생이 전혀 무관할 때

    - $P(A\cap B)=P(A)P(B)$
    - $P(A|B)=P(A)$ 사건 B의 발생 여부가 사건 A의 발생에 영향을 주지 않는다는 독립의 개념을 잘 설명해 줌
    - 독립이면 $P(A\cap B)=P(A)P(B)$, 배반이면 $(A\cap B)=∅$이므로 $P(A\cap B)=0$이 됨

    - 두 사건의 확률이 모두 양수라면 독립과 배반의 조건을 동시에 만족시킬 수 없음

 

- 표본공간의 분할(partition): 배반사건들의 모임

(https://www.youtube.com/watch?v=4zptP2UNdCE&t=121s 참고하여 작성)

표본공간의 분할 (https://www.youtube.com/watch?v=4zptP2UNdCE&t=121s 참고하여 작성)

 

- 총확률의 법칙(law of total probability)

    - 곱사건의 확률법칙과 사건의 분할을 이용하여 임의의 사건의 확률을 표현한 것

   - e) 어떤 공장의 제품이 30%는 A1공장, 50%는 A2공장, 20%는 A3공장에서 생산되며, 각 불량률이 2%, 1%, 5%일 때, 임의로 하나를 뽑았더니 불량일 확률 $P(B) = 0.021$

    - 아래 그림에서 $B$ 부분의 확률을 구할 때 총확률법칙 사용

총확률의 법칙 표본공간의 분할 (https://www.youtube.com/watch?v=4zptP2UNdCE&t=121s 참고하여 작성)

 

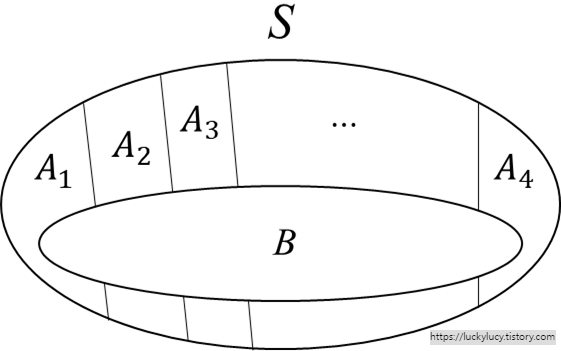
    - 총확률의 법칙 증명

$$B=B\cap S$$

$$=B\cap(A_1\cup A_2\cup A_3\cup \cdots \cup A_k)$$

$$=(B\cap A_1)\cup (B\cap A_2)\cup \cdots \cup (B\cap A_k)$$
        그런데 $(B\cap A_k)$끼리는 배반이므로,

$$P(B)=P[(B\cap A_1)\cup (B\cap A_2)\cup \cdots \cup (B\cap A_k)]$$

$$=P[(B\cap A_1)+(B\cap A_2)+\cdots+(B\cap A_k)]$$

$$= \sum_{i=1}^{k}P(B\cap A_i)$$

$$= \sum_{i=1}^{k}P(A_i)P(B|A_i)$$

 

- 베이즈 정리

    - 어떤 사건의 발생 확률에 대한 선험적 생각이 실험에 의해 변화되는 체계적 과정을 표현

   - e) 어떤 공장의 제품이 불량일 때 A1공장에서 만들어졌을 확률 $P(A_1|B) = 0.28571$

   - 그림에서 전체 $B$를 알 때, $P(A_i|B)$(그림에서 색칠한 부분)를 추정할 때 사용

베이즈 정리 (https://www.youtube.com/watch?v=4zptP2UNdCE&t=121s 참고하여 작성)

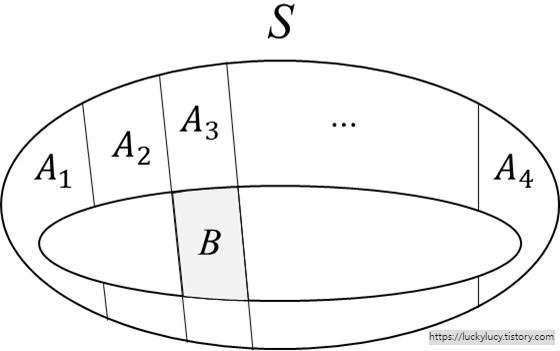
   - 사건 $A_1, A_2, \cdots, A_n$이 표본공간의 분할일 때, 임의의 사건 $B$에 대하여 다음 식이 성립
        $P(A_i|B)=\frac{P(A_i)P(B|A_i)}{P(A_1)P(B|A_1)+\cdots +P(A_n)P(B|A_n)}, i=1, \cdots, n$

 

 

 

통계학: 파이썬을 이용한 분석

오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파이썬은 빅데이터 처리에서 가장 많이 쓰이는 고급 프로그래밍 언어 중 하나로서 인터넷을 통해 무료로 또한, 지속적으로 새로운 함수 등이 업데이트되고 있어서 실제로 트렌디한 데이터 분석 및 여러 인공지능 관련 프로그래밍에서 필수적인 언어로 자리매김하는 중이다. 각 장 마지막 부분에는 파이썬을 이용한 예제를 제시하여 그 장에서 소개한 내용에 대한 예제를 따라하면서 언어와 분석 방법을 익힐 수 있도록 구성하였으며, 기본적인 파이썬에 대한 사용법은 부록에 수록하였다.

저자

인하대학교 통계학과

출판

자유아카데미

출판일

2022.06.25