[기초통계] 확률분포(확률변수, 이산확률변수와 확률분포, 확률분포의 기댓값과 표준편차, 두 확률변수의 결합분포, 공분산과 상관계수, 두 확률변수)

<통계학 : 파이썬을 이용한 분석> 책 내용 중 '6장. 확률분포' 부분을 요약하였고, 필요한 내용은 더 추가한 글임을 미리 밝힙니다.

 

6. 확률분포

6.2 확률변수

- 확률변수(random variable): 각 근원사건에 실숫값을 대응시키는 함수이며 $X, Y, \cdots$로 표시
- 이산확률변수: 확률변수가 가질 수 있는 값이 유한하거나 무한하더라도 셀 수 있는 경우
- 연속확률변수: 연속적인 구간에 속하는 모든 값을 다 가질 수 있는 경우

---

6.3 이산확률변수와 확률분포

- 확률분포(probability distribution)
- 확률변수가 갖는 값과 그 값을 가질 확률을 정해주는 규칙 또는 관계
- 보통은 확률변수 $X$의 분포라고 함


- 확률함수, 확률질량함수(probability mass function)
- 확률변수 $X$가 $k$개의 값 $x_1, x_2, \cdots, x_k$를 가질 때 그에 대응하는 확률을 $f(x_1), f(x_2), \cdots, f(x_k)$로 표현
- 이산확률변수 $X$의 확률함수 $f(x_i)=P(X=x_i)$는 다음 조건을 만족해야 함
- (1) 모든 $x_i$값에 대해 $0\leq f(x_i)\leq 1$
- (2) $\sum_{모든 x_i}f(x_i)=1$

 

X	1	2	3	4	5	6	합
P(X)	1/6	1/6	1/6	1/6	1/6	1/6	1

이산확률분포표 예시

 

---

6.4 확률분포의 기댓값(평균)과 표준편차

- 기댓값(expected value)
- 확률분포의 중심을 나타내는 수치로 $E(X)$ 또는 $μ$로 표현
- 모집단의 평균 $E(X)=\sum$ (확률변수가 취하는 값 $\times$ 그 값을 가질 확률)$=\sum x_if(x_i)$


- 표준편차(standard deviation)
- 확률분포의 퍼진 정도를 나타내는 수치
- 표준편차($σ$)의 단위는 확률변수 $X$의 단위와 동일하므로 분산($σ^2$)보다 퍼진 정도를 측정하는 데 더 적절함
- $X$의 분산 $Var(X)=E(X-μ)^2=\sum(x_i-μ)^2f(x_i)$
- $X$의 표준편차 $sd(X)=\sqrt{Var(X)}$
- 분산의 계산식 $Var(X)=E(X^2)-(E(X))^2=\sum x_i^2f(x_i)-μ^2$

 

---

6.5 두 확률변수의 결합분포

- 결합확률분포(joint probability distribution)
- 키와 몸무게 등 두 개 이상의 항목을 관측할 때 특성 간 관계 여부, 관계 정도 등을 이해하기 위해 결합확률분포 이해 필요
- $X$가 취하는 값과 $Y$가 취하는 값의 각 쌍에 대응하는 확률
- e) 자동차 10대 중 5대는 정상, 2대는 기어변속기에 문제가 있고, 3대에는 엔진에 문제가 있음. 임의로 차를 골랐을 때 기어변속기에 문제가 있는 차와 엔진에 문제가 있는 차를 고르게 될 확률들
- 두 개의 확률변수가 이산일 경우, $X$가 취하는 값을 $x_1, \cdots, x_m$, $Y$가 취하는 값을 $y_1, \cdots, y_n$이라고 할 때 $X$와 $Y$의 결합확률 분포는 모든 $1\leq i\leq m, 1\leq j\leq n$에 대하여 $f(x_i, y_i)=P[X=x_i, Y=y_j]$를 구함으로 결정됨


- 주변확률분포(marginal probability distribution)
- 확률들이 이론적으로 계산되지 않을 경우 상대도수의 수렴치로 확률을 계산
- $X$나 $Y$ 하나만 문제가 되는 경우의 확률, 기댓값, 표준편차 등 계산에 이용
- $X$와 $Y$의 주변확률분포는 다음의 주변확률에 의해 결정됨
- $f_X(x_i)=P[X=x_i]=\sum_{j=1}^{n}f(x_i, y_j)$
- $f_Y(y_j)=P[Y=y_j]=\sum_{i=1}^{m}f(x_i, y_j)$

---

6.6 공분산과 상관계수 - 공분산(covariance)
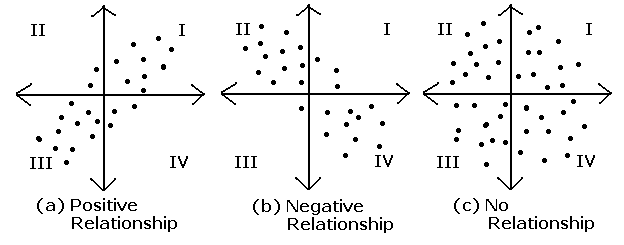
- 두 개의 확률변수 $X$와 $Y$가 어떤 관계를 가지며(양의 관계 or 음의 관계) 변화하는지 나타내는 척도로, $E(X-μ_X)(Y-μ_Y)$로 정의됨
- 같은 방향으로 커진다면 양수, 다른 방향으로 커진다면 음수의 기댓값을 갖게 됨
$$Cov(X,Y)=E(X-μ_X)(Y-μ_Y)$$
$$E(XY)-μ_Xμ_Y$$
이때, $$E(XY)=\sum_{i=1}^{m}\sum_{j=1}^{n} x_iy_jf(x_i,y_j)$$

공분산 예시 (출처: https://destrudo.tistory.com/15)

- 상관계수(correlation coefficient)
- 공분산 값은 X, Y 단위의 영향을 받기 때문에, 이러한 특징을 제거하기 위해 제안됨
- $Corr(X,Y) = \frac{Cov(X,Y)}{σ^Xσ^Y}$
- 상관계수의 성질
- (1) $X$와 $Y$의 상관계수는 항상 -1과 1 사이의 값을 가짐. 정확한 선형관계 $Y=aX+b$가 성립할 때 상관계수 값은 1 또는 -1
- (2) $X$와 $Y$의 상관계수는 각 확률변수에 상수가 더해지거나 감해지는 것에 영향을 받지 않으며, 상수가 곱해진 경우에는 그 부호에만 영향을 받음. 즉 0이 아닌 임의의 $a, b$에 대해 $Corr(aX,bY)=[ab의 부호]Corr(X,Y)=\frac{ab}{|ab|}Corr(X, Y)$

 

---

6.7 두 확률변수의 독립성

- 두 사건 $A$와 $B$가 독립이 되기 위하여 $P(A\cap B)=P(A)P(B)$를 만족시켜야 함
- 비슷한 논리로, 두 개의 확률변수 $X$와 $Y$가 독립이 되기 위해서는 $X$와 $Y$가 취하는 모든 쌍의 값 $(x_i, y_j)$에 대해 $f(x_i, y_j)=f_X(x_i)f_Y(y_i)$를 만족시켜야 함
- 즉, $x_i$와 $y_j$가 동시에 일어나는 확률 = 각 확률변수가 일어날 확률의 곱

- 예제 13. 동전을 세 번 던지는 실험에서 X는 처음 두 번 던질 때 나오는 앞면의 수, Y는 세 번째 던질 때 나오는 앞면의 수
(두 확률변수가 독립인 경우)

x, y	0	1	2	$f_Y(y)$
0	1/8	1/4	1/8	1/2
1	1/8	1/4	1/8	1/2
$f_X(x)$	1/4	1/2	1/4	1

$$f_X(2) \times f_Y(1)=f(2, 1)$$ $$1/4 \times 1/2=1/8$$

- 예제 10. 차 10대 중 5대는 정상, 2대는 기어변속기 고장, 3대는 엔진에 문제가 있음. 10대 중 2대를 뽑을 경우
(두 확률변수가 독립이 아닌 경우)

X	1	2	3	4	5	6	합
P(X)	1/6	1/6	1/6	1/6	1/6	1/6	1

$$f_X(0) \times f_Y(0)\neq f(0, 0)$$
$$28/45\times 21/45=0.29\neq 0.22$$

- 두 개의 확률변수 X, Y가 독립일 때
- $E(XY)=E(X)E(Y)$
- 증명
$$E(XY)=\sum_{i=1}^{m}\sum_{j=1}^{n}x_iy_jf(x_i,y_j)$$
두 확률변수가 독립이면, $x_iy_jf(x_i,y_j) = f_X(x_i)f_Y(y_j)$
$$=\sum_{i=1}^{m}\sum_{j=1}^{n}x_iy_jf_X(x_i)f_Y(y_j)$$
$$=\sum_{i=1}^{m}x_if_X(x_i)\sum_{j=1}^{n}y_jf_Y(y_j)$$
$$=E(X)E(Y)$$
- 이 식으로부터 독립성이 공분산과 상관계수를 0으로 만들어 줌
- $Cov(X,Y)=0, Corr(X, Y)=0$
- 그러나, 공분산과 상관계수가 0이더라도 두 변수가 독립이 되는 것은 아님

- 예제 14. 두 확률변수 X, Y의 결합분포가 아래와 같음(공분산은 0이지만 독립이 아닌 경우)

x, y	-1	0	1	$f_Y(y)$
0	0	1/3	0	1/3
1	1/3	0	1/3	2/3
$f_X(x)$	1/3	1/3	1/3	1

- (1) 공분산
$$Cov(X,Y)=E(X,Y)-μ_Xμ_Y$$
$$=[(-1)\times \frac{1}3 + (1)\times \frac{1}3]-[\frac{2}3 \times 0]$$
$$= 0$$

- (2) 독립?

$$f(0,0) = 1/3 \neq f_X(0)f_Y(0)=1/3\times 1/3 =1/9$$

- $(X+Y)$의 분산을 구하는 법
- 분산의 정의: 관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눈 것
$$Var(X+Y)=E[(X+Y)-E(X+Y)]^2$$ $$=E[(X-E(X))+(Y-E(Y))]^2$$ $$=E[(X-E(X))^2]+2E[(X-E(X))(Y-E(Y))]+E(Y-E(Y))^2]$$
이때 분산과 공분산의 정의를 이용하면 ($E[(X-E(X))^2]=Var(X)$)
$$Var(X+Y)=Var(X)+2Cov(X,Y)+Var(Y)$$
- 두 확률번수가 독립인 경우, 공분산이 0이 되므로 $Var(X+Y)=Var(X)+Var(Y)$로 표현

 

 

통계학: 파이썬을 이용한 분석

오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파이썬은 빅데이터 처리에서 가장 많이 쓰이는 고급 프로그래밍 언어 중 하나로서 인터넷을 통해 무료로 또한, 지속적으로 새로운 함수 등이 업데이트되고 있어서 실제로 트렌디한 데이터 분석 및 여러 인공지능 관련 프로그래밍에서 필수적인 언어로 자리매김하는 중이다. 각 장 마지막 부분에는 파이썬을 이용한 예제를 제시하여 그 장에서 소개한 내용에 대한 예제를 따라하면서 언어와 분석 방법을 익힐 수 있도록 구성하였으며, 기본적인 파이썬에 대한 사용법은 부록에 수록하였다.

저자

인하대학교 통계학과

출판

자유아카데미

출판일

2022.06.25